Aerodynamics Matter Regardless How Fast a Car Goes
The claim: Drag only matters if you go above a
certain speed. 45 mph/50 mph/55 mph/60 mph—take your pick, as the critical
speed depends entirely on the person reporting this myth.
The reality: People who repeat this claim are telling
only part of the story—as is true of many, if not all, of these misconceptions.
To see why, we need to go back (again) to some fundamentals of fluids in
motion.
If you’ve ever taken a college physics class, you might
remember something called the “Bernoulli equation.” This equation describes the
relationship between internal energy, potential energy, and kinetic energy in a
fluid—not just a fluid in motion, but any (incompressible) fluid (e.g.
the “hydrostatic equation” is the Bernoulli equation simplified for a static fluid). By
definition, the specific volume, v, of an incompressible fluid must
remain constant, allowing us to divide out volume, V, and convert the
energy terms into pressures. Because energy is conserved (that is, it is
neither created nor destroyed), the sum of internal energy + potential
energy + kinetic energy must be constant in a system if no
energy flows cross the system boundary and if mass flow in = mass flow out
(that is, the system is in steady state). In mathematical terms,
Assuming no energy is added or taken away from the system
(and assuming an incompressible fluid, etc.), this relationship should hold
true.
You might recognize one of these terms from the equation for
aerodynamic drag force (which is one component of total aerodynamic force,
acting parallel to the car’s centerline): One-half of the product of density and the square of velocity
is something we call “dynamic pressure,” and it is, as its form suggests,
simply the kinetic energy of an incompressible flow with volume divided out (recall that the kinetic energy of a solid is
equal to one half of the product of its mass and the square of its velocity.
Dividing mass m by volume V gives density ρ; the
inverse of this, V/m, is specific volume, v). In ground vehicle
aerodynamics, gravity can (usually) be ignored since its effect on airflows is negligible when considering the flow around a car.
This leaves a modified form of Bernoulli’s equation, As you might guess, this is where the negative relationship
between pressure and velocity is described: as one goes up, the other must go down
to satisfy the equation. Rewriting the equation makes this clearer: 
Consequently, measuring panel pressures on a moving car tells you something about the airflow at that
location, namely whether it is faster (negative gauge pressure) or slower (positive gauge pressure) than the car’s speed.
Now let’s look at the kinetic energy term, or dynamic
pressure, specifically. This is proportional to the square of velocity, and
since aerodynamic force is directly related to dynamic pressure, drag is also
proportional to the square of the flow velocity. This means that as a car’s
speed increases, the aerodynamic drag it must overcome goes up dramatically
faster. A car traveling at 60 mph must overcome 4 times as much aerodynamic
drag as it did at 30 mph, even though its speed has only doubled.
The other force fighting a car in motion is what we call
“rolling” or “mechanical” drag, which includes things like the friction and
inertia of rotating engine and driveline components such as axles, wheels, and
tires. At low speeds, aerodynamic drag is a much smaller proportion of the
total resistance acting against a car than mechanical drag, and depending on
the car (and especially how much mass it has, how big it is, and how it is
shaped), they can be equal anywhere between, roughly, 40-60 mph. If that seems
like a wide range, well—there are a lot of different cars out there, from tiny
hatchbacks to hulking pickup trucks to Class 8 tractor-trailers, with widely varying drag characteristics. So,
the first problem with the assertion that aerodynamic drag “doesn’t matter”
below a certain speed is that the speed where aerodynamic drag becomes
predominant will vary depending on the car. A blanket statement pinpointing one
exact speed for every car or truck is simply incorrect.
The second problem is aerodynamic drag varies continuously.
Say we’re looking at a car where aero drag equals mechanical drag at 60 mph.
Well, what about at 59 mph? Aero drag is still almost equal to
mechanical drag at that speed in our hypothetical car. How about 58 mph? 57
mph? 56 mph? Would reducing the drag coefficient of the car still “matter” at 55
mph even though at that speed aerodynamic force is only around 85% as large as
mechanical resistance?
|
Drag doesn’t suddenly matter at 60 kph—it isn’t an on/off switch. (Also, this should read "its relationship to speed is not directly proportional"—since it is proportional to speed squared!).
|
I would argue it does; resistive force is resistive force.
Cut the car’s speed in half, to 30 mph, and now you might be able to make a
case for ignoring improvements to its aerodynamic performance since that aero
drag is now only 25% as large as mechanical drag in our hypothetical example (at the same time, what car
only gets driven at 30 mph? Okay, aside from Supermileage bullet cars:
 |
| Even though they race at low speeds, these cars are optimized for low aerodynamic drag. Since they are also very lightweight, aero drag might be as much or more than mechanical drag, even at low speed. (Image credit: https://ecoillini.mechse.illinois.edu/). |
...and bicycles. The effects of aerodynamic drag--especially how it changes with body position and headwinds--can be easily felt on a bicycle, and measured. For example, my best 40 km time trial on this bike:
...was 62 minutes. However, on this bike:
...that improved to 56 minutes, more than 4 kph faster).
But there is no discrete point at which aero drag “matters”
and below which it doesn’t, only a speed above which aero drag predominates
and below which it doesn’t but may still be substantial. And keep in mind, that
critical speed is different (and usually unknown without sophisticated measuring
equipment) for every car model.
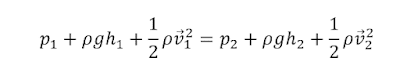
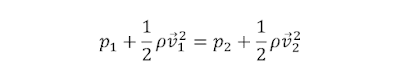
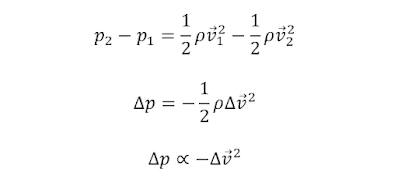
Comments
Post a Comment