Systems
engineering has a long history despite not becoming a formalized discipline
until after World War 2. What is systems engineering? Basically, it is the overarching
management of large or complex design projects: identification of customer
needs and market, development of requirements, control of subsystems and
integration, etc. For example, how is a modern airliner built? First, a
preliminary design study is completed, often lasting a few years, before
requirements are finalized and the basic design of the vehicle is established;
then, detailed design work can begin, which usually takes several years to
complete. Finally, verification and certification testing are completed, after
which the vehicle can be released. All these processes are overseen by systems engineers.
 |
| The evolution of automotive systems engineering in one picture. As time goes on, the product is more technically complex and requires more rigorous control of various inputs in the design process. |
Similarity
Analysis
One of the
starting points for basic design of a new vehicle is similarity analysis,
the evaluation of existing vehicles that serve the same market or purpose as
the proposed new design. In similarity analysis, one must identify important
parameters or characteristics of competitor vehicles; oftentimes, these are proprietary
and must be estimated. We have spent a considerable amount of time practicing
this with aerospace vehicles in my Systems Designs class this semester, but
since my primary interest is in ground vehicles I started collecting
information on production automobiles in a spreadsheet to see what I could
learn.
Specifically,
after looking at aerodynamic and dimension data for a bunch of cars, and after this
topic was brought up in class last week, I started to wonder: can we answer the
question of whether a 100-mpg gas-powered car—long the “holy grail” of the auto
industry—is possible by conducting a basic similarity study?
You’ve
probably heard of the concept of the 100-mpg car before, since it was
popularized by the “Automotive X-Prize” competition that ran for several years
about a decade ago. Nothing ultimately came of that competition—the mass-produced 100-mpg gas
car has never been a reality. Let’s find out why.
Methodology
In order
to try and answer this question, I first identified what data I would need. To
do this, we ask: “What drives fuel consumption in a car?” A good starting point
to answer a question like this is a free body diagram, a
visual plot of the forces acting on a body and their directions. Do this for a
car in motion and you will figure out that fuel consumption (which is really a
proxy for energy usage) is driven by rolling drag and aerodynamic drag. What
are the primary factors driving these two forces? Weight, drag area, and
velocity have the largest influence, with secondary drivers being coefficient
of rolling resistance, air density, gravitational acceleration (we usually
neglect it in calculations, but this varies with altitude), elevation changes,
and atmospheric conditions (especially wind). For simplicity of analysis, some
of these secondary effects can be ignored; here, I will assume negligible elevation
changes, air density and gravitational acceleration at sea level, and no winds.
You may
have read in car reviews that a manufacturer says their new car model uses “X
horsepower at Y mph.” How is this calculated? Power is given by the tractive
force exerted by a car multiplied by its velocity; in SI basic units this returns
power in watts (W) but standard units in automotive engineering are “horsepower”
(hp). At cruise, the tractive force required to maintain speed is the same as
the total resistive force acting on the car (since change in velocity is 0), or
the sum of rolling and aerodynamic drag. Aerodynamic drag is given by the
familiar equation…and
rolling drag by the weight multiplied by some coefficient of rolling
resistance, typically between 0.010 and 0.015 for a car tire (LRR tires being
on the low end and knobby off-road tires on the high end). To account for the
inertial moments of the rotating components of a car—wheels/tires, brakes,
axles, transmission gears, crankshafts, etc.—nominal weight is multiplied by a correction
factor. I have previously tried to calculate this for my car and arrived at an estimate of 2% of total mass; I will assume this correction factor for all the vehicles below. This gives rolling drag by Add these
two together and multiply by cruise speed et voilá: horsepower required.
To check the validity of this method, you can compare it against one of those
reported values from the auto magazines. For example, when the Volkswagen XL1
was released (in very limited numbers) back in 2014, it was widely reported
that VW said it required 8.3 hp to maintain 62 mph—still an absurdly low
number! VW’s press materials gave the weight, drag coefficient, and dimensions
of the XL1 so, using standard atmosphere, we can calculate required power with
our equation and check it against the reported value:
How about
that—exactly the same! In fact, this is probably how VW engineers calculated
the required horsepower. You can do the same for your car. (Note that I will include 150 lb driver weight in all calculations below; VW may not have done that, or they may have used a lower coefficient of rolling resistance).
Now, let’s
do this for a bunch of cars. Dimensions and weights are very easy to find for
any current car; manufacturers usually publish this right on their websites.
Only a handful of OEMs publish drag coefficients, however, and some are very
inconsistent about it, doing it for some of their cars and not others (*cough*
Toyota *cough*). However, after a couple days of intermittent searching and
procrastinating homework I was able to find reliable (as in, from a reputable
source—either the manufacturer directly or a reliable automotive news source
like Car & Driver) drag coefficients for about 30 cars, a fairly
broad selection of everything from economy cars to large trucks (mostly 2024 or
2025 model year, but I included older if the generation hasn’t changed, as well
as a 2006 Insight and 2013 Prius for reference). It was sometimes a surprise which
data manufacturers choose to include—for instance, Stellantis lists frontal
area in the specifications data of the 2022 Jeep Grand Cherokee! If you go
looking for this yourself, a good place to start is press packages from new car
introductions; often, aerodynamic data will be included in the info dump.
Then,
throw it all in a spreadsheet with the proper formulas and propagate it with calculated
values. You should get something that looks like this:
 |
| Yes, I am a nerd who does this for fun and I fully embrace that. |
That’s a
lot of information, and very hard to glean anything about trends despite
organizing it by ascending cruise horsepower. I’ve written before that plotting
things visually helps to see what you’re interested in learning from the data. Let’s do that here.
Results
What
should we plot? Well, I’m interested in seeing how fuel economy trends with its
drivers, which I identified above as velocity, drag area, and weight. Since I’m
comparing these vehicles at constant cruise, velocity has been removed as a
variable, leaving weight and drag area. Let’s graph EPA highway fuel economy as
a function of each of those:
There are definite
trends here, although correlation is not as high as I would have hoped (R2
= 1 would mean the interpolated line crosses through every data point).
However, it’s clear that generally, as weight or drag area increase, EPA
highway fuel economy goes down.
But
remember, drag area and weight each factor into the same parameter: cruise
power. What happens if we graph EPA highway fuel economy as a function of
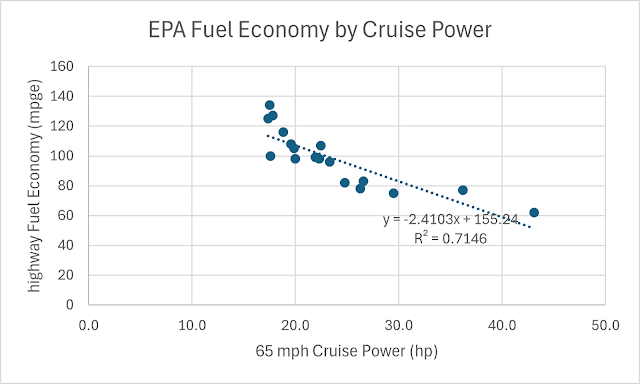
required horsepower at cruise?
Now the
trend is even clearer, and correlation is higher: as required cruise horsepower
goes up, EPA highway fuel economy goes down.
Discussion
I’m not
surprised that the plots show this correlation between weight, drag area, cruise
power, and fuel economy; it’s exactly what we expect based on intuition. More
power required to go the same speed = more fuel required.
Much of
the variation can be explained by the fact that a variety of cars are
represented. For example, these two points:
…are the Toyota
GR86 and Nissan GT-R. While their weights and drag areas are fairly low, the
cars are optimized for track performance more than economical driving, with
things like shorter gearing helping acceleration but putting their engines in
higher-consumption parts of their fuel maps at cruise. On the other side, this
point:
…is the
2006 Honda Insight, still the lowest-drag car ever sold in the US. That car was
optimized in an entirely different way, specifically to get good fuel economy.
This is even more true of the XL1, which sits here on the plot (estimating its
highway cruise at 100 mpg, on the low end of what magazine reviews said it got;
this car was never sold in the US and consequently has no EPA rating):
Now, the
problem with the XL1 and original Insight is their optimization: both cars are
two-seaters, are made of lightweight but expensive materials, and do not have
the typical capabilities buyers generally expect in a car e.g. four doors, seating
for 5, sound insulation (XL1), etc. So, both cars were short-lived, did
not sell in large numbers (the XL1 by design), did not spawn imitators, and did
not have much lasting impact on car design. They’re really outliers here.
And that
leads me to conclude that we will never see a 100-mpg gas-powered car for sale
in the US. In order to achieve that, such a car would have to be very light
(increasingly hard with more mandated safety equipment now than even 10 years
ago), very small (which buyers consistently demonstrate they do not prefer, as
they have gravitated over the last several decades to larger and larger trucks and SUVs),
and very compromised in terms of what buyers want. To make a business case, a
new car can’t stray very far from the mainstream. Extrapolate the graphs above
to their y-axes and the intercept is only around 70 mpg on each of them. Of
course, in reality there is a hard weight limit somewhere, probably around 2000
lb based on production cars in the last half century. As we get nearer that
weight limit and some minimum drag area (a respected aerodynamicist told me
once that he thinks production cars will achieve CD = 0.20
and pretty much stop there), the only gains possible will be from increased
efficiency in the engine and drivetrain, and that is subject to physical
limits too. This tells me that, for a gas car that could be saleable
and is reasonably close to providing the same capabilities and user experience
as today’s cars, 100 mpg is simply not feasible.
Now, where
we do have 100-mpg gas-equivalent cars is in the electric market.
Due to the inherent efficiency advantage of electric motors compared to combustion
engines (which waste more than half the energy in the liquid fuel as unusable
heat), many EVs get the equivalent of 100 mpg or more. Plotting EPA economy as
a function of required cruise power (using the same methodology as above) but
this time for EVs might show us something interesting too.
Notice
that the high ends of both weight and cruise power are greater than on the ICE
graphs (the heaviest vehicle on each list is the Chevrolet Silverado, which has
both gas and electric versions), a consequence of EVs tending to be heavier
than their ICE counterparts due to their use of large batteries to provide
consumer-acceptable range and consequently requiring more power to sustain any
given speed. These plots suggest that weight must be kept low for EVs to
achieve best efficiency.
Thinking about
that led me to wonder if the proportion (percentage) of aerodynamic drag and
rolling drag would show any trends. Here are plots of the relative proportions
as functions of weight, drag area, and cruise power for gas cars and EVs
combined:
The last two charts don’t show much correlation; as drag area or required power
increase, there doesn’t appear to be any real trend in in the relative importance of
aero fraction versus rolling fraction. But that first chart does show a clear
trend: lighter cars tend to have a greater portion of their energy devoted to overcoming
aerodynamic drag—and so will benefit more from measures to reduce drag area
than weight. On the other hand, as cars get heavier a larger proportion of
their energy is used to overcome rolling drag—so these cars may benefit more
from measures to reduce weight. Again, we sort of know this intuitively but charting
a cross section of actual cars shows it objectively. That’s the lesson of
similarity analysis, and it echoes a sentiment I’ve shared on this site many
times before: don’t guess! Look at what’s actually going on.
 |
| The 2014 Volkswagen XL1; you can see this example at the Lane Motor Museum in Nashville, TN. |




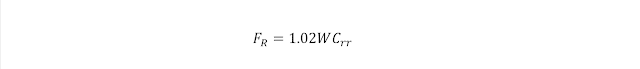
















Comments
Post a Comment